Unlocking The Mystery: What Does X*X*X Truly Equal?

Have you ever stared at a mathematical expression like "x*x*x is equal to" and felt a mix of curiosity and confusion? Perhaps you've encountered it in a textbook, a problem-solving challenge, or even a real-world scenario. This seemingly simple string of 'x's holds a fundamental concept in algebra, representing a powerful operation that underpins much of our modern understanding of science, engineering, and data. It's more than just a sequence of letters; it's a gateway to understanding how quantities relate and how we can find unknown values that drive countless systems around us.

In the world of mathematics, particularly algebra, the expression "x*x*x is equal to" introduces us to the concept of exponents, specifically cubing a variable. This isn't just an abstract academic exercise; it's a practical tool for describing volumes, growth rates, and complex relationships in diverse fields. From calculating the space a three-dimensional object occupies to modeling economic trends or physical phenomena, understanding what "x*x*x is equal to" means and how to solve for 'x' is an invaluable skill. Join us on a journey to demystify this intriguing algebraic statement, explore its profound implications, and learn how to unlock its secrets.

Table of Contents

• Understanding the Core: What the Equals Sign Really Means
• The Power of Three: Unraveling X*X*X
  • From Multiplication to Exponents: The Shorthand of Power
  • Visualizing the Cube: Why "Cubed" Makes Sense
• Solving for X: The Art of Balancing Equations
  • General Principles of Equation Solving
  • Tackling the Cubic Challenge: Solving X*X*X Equations
• Case Study 1: When X*X*X is Equal to 2
• Case Study 2: When X*X*X is Equal to 2023
• Real-World Applications: Where X*X*X Shines
• The Role of Technology in Solving Complex Equations
• Beyond Real Numbers: The Intriguing World of Complex Solutions

Understanding the Core: What the Equals Sign Really Means

At the heart of any equation, including one involving "x*x*x is equal to," lies the humble yet profound equals sign (`=`). An equation, by its very definition, is a statement that two expressions are equal. It declares a perfect balance, much like a seesaw where the weight on one side precisely matches the weight on the other. For instance, in the equation `2x + 3 = 7`, the expression `2x + 3` must hold the exact same value as `7`. Our goal in solving such an equation is to find the value of the unknown variable, 'x', that makes this statement true. This concept of equality is not just a mathematical convention; it's a fundamental principle that allows us to model and understand the world around us. Whether we're calculating the trajectory of a rocket, designing a bridge, or balancing a budget, the idea that certain quantities must be equivalent for a system to work correctly is paramount. When we encounter "x*x*x is equal to" a certain number, we are essentially looking for a specific value of 'x' that, when multiplied by itself three times, achieves that exact numerical balance. It’s a quest for the unique input that yields a desired output, a common theme in all problem-solving endeavors.

The Power of Three: Unraveling X*X*X

The expression "x*x*x is equal to" is a direct representation of a mathematical operation called cubing. In essence, it means multiplying the variable 'x' by itself, and then multiplying the result by 'x' one more time. This repeated multiplication has a special shorthand in algebra, known as exponents.

From Multiplication to Exponents: The Shorthand of Power

Instead of writing out `x*x*x`, mathematicians use a more concise notation: `x^3`. This is read as "x raised to the power of 3" or simply "x cubed." The small number `3` written as a superscript is called the exponent, and it tells us how many times the base number (in this case, 'x') is multiplied by itself. So, `x^3` is mathematically equivalent to `x*x*x`. This compact notation is not just for convenience; it allows for clearer representation of complex mathematical relationships and makes calculations more manageable, especially when dealing with higher powers. For instance, imagine writing `x*x*x*x*x*x*x*x*x*x` instead of `x^10`! The efficiency of exponential notation is undeniable.

Visualizing the Cube: Why "Cubed" Makes Sense

The term "cubed" isn't arbitrary. It directly relates to geometry. If 'x' represents the length of one side of a perfect cube, then `x*x` (or `x^2`) represents the area of one of its faces. Extending this, `x*x*x` (or `x^3`) represents the total volume of that three-dimensional cube. This geometric interpretation provides an intuitive understanding of what `x^3` signifies: it's a measure of three-dimensional space, a concept crucial in fields ranging from architecture to physics. When we talk about "x*x*x is equal to" a certain number, we are often implicitly asking for the side length of a cube that would have that specific volume.

Solving for X: The Art of Balancing Equations

Solving an equation means finding the value(s) of the unknown variable that make the equation true. Whether it's a simple linear equation or a complex cubic one like "x*x*x is equal to" a given number, the underlying principle remains the same: maintaining balance.

General Principles of Equation Solving

The core idea behind solving any equation is to isolate the variable on one side of the equals sign. This is achieved by applying inverse operations to both sides of the equation, ensuring that the balance is always maintained. Think back to the seesaw analogy: whatever you do to one side, you must do to the other to keep it level. For example, to solve a simple linear equation like `2x + 3 = 7`: 1. **Subtract 3 from both sides:** This cancels out the `+3` on the left, leaving `2x = 4`. 2. **Divide by 2 on both sides:** This isolates `x`, giving `x = 2`. These steps, though simple, embody the fundamental rules of algebra: addition undoes subtraction, multiplication undoes division, and vice versa. When dealing with "x*x*x is equal to" a number, we're looking for the inverse operation of cubing, which is taking the cube root.

Tackling the Cubic Challenge: Solving X*X*X Equations

When we encounter an equation like `x*x*x = N` (where N is some number), we are looking for the cube root of N. The cube root operation is represented by the symbol `∛`. So, if `x^3 = N`, then `x = ∛N`. Unlike square roots, which can yield both positive and negative real numbers (e.g., the square root of 4 is both 2 and -2), a real cube root of a number has only one real solution. For instance, `∛8 = 2` because `2*2*2 = 8`. Similarly, `∛-8 = -2` because `(-2)*(-2)*(-2) = -8`. This characteristic simplifies finding the real solution for `x` in `x*x*x` equations. However, it's important to note that cubic equations, in general, can have up to three solutions (roots), which may include complex numbers, a concept we'll touch upon later. For many practical purposes, finding the single real root is sufficient.

Case Study 1: When X*X*X is Equal to 2

Let's consider the intriguing equation: `x*x*x is equal to 2`. This can be written as `x^3 = 2`. To solve for `x`, we need to find the cube root of 2. `x = ∛2` The number `∛2` is an irrational number, meaning its decimal representation goes on infinitely without repeating. Its approximate value is `1.25992104989...`. This numerical constant is unique and holds significant importance in various mathematical and scientific contexts. For example, it's related to the problem of "doubling the cube," an ancient geometric problem. The fact that the solution is irrational highlights that not all problems have neat, whole-number answers, pushing the boundaries of our understanding of numbers themselves. This equation, `x*x*x is equal to 2`, serves as a perfect example of how algebraic problems can lead us to discover and work with numbers that extend beyond simple integers or fractions.

Case Study 2: When X*X*X is Equal to 2023

Another compelling example is the equation `x*x*x is equal to 2023`. This translates to `x^3 = 2023`. To find the value of `x`, we again apply the cube root operation: `x = ∛2023` Calculating this without a calculator can be challenging, as 2023 is not a perfect cube. Using a calculator, we find that `x ≈ 12.6444`. This value, when multiplied by itself three times, will approximately yield 2023. The steps to calculate `x*x*x is equal to 2023` involve first writing the equation in its simplest form, `x^3 = 2023`, and then applying the cube root. This problem, like `x*x*x is equal to 2`, demonstrates the need for tools beyond mental arithmetic or simple factorization when dealing with non-perfect cubes. It underscores the practical utility of calculators and computational methods in modern problem-solving.

Real-World Applications: Where X*X*X Shines

The concept of "x*x*x is equal to" extends far beyond the classroom, finding critical applications across a multitude of disciplines. Its ability to model three-dimensional relationships and growth patterns makes it indispensable. * **Engineering:** Engineers frequently use cubic equations. For instance, when designing structures, they might need to calculate the volume of materials, the stress on a beam, or the flow rate in pipes, all of which can involve cubic relationships. The strength of certain materials under load can be modeled by equations where `x^3` plays a crucial role. * **Physics:** In physics, `x^3` appears in formulas for volume (as discussed), but also in more complex scenarios like gravitational potential energy or fluid dynamics. For example, the volume of a sphere is proportional to the cube of its radius (`(4/3)πr^3`), and understanding this relationship is vital for everything from astronomy to designing pressure vessels. * **Economics:** Economists use cubic functions to model supply and demand curves, cost functions, or even population growth. While often simplified, more complex economic models can incorporate cubic terms to represent diminishing returns or non-linear relationships between variables. Understanding "x*x*x is equal to" a certain economic output can help in forecasting and policy-making. * **Chemistry:** In chemistry, `x^3` might appear in calculations related to reaction rates, gas laws, or the properties of crystalline structures. For example, the volume occupied by a certain amount of gas under specific conditions might be described by an equation involving a cubic term. * **Mathematics:** Beyond basic algebra, cubic equations are a cornerstone of advanced mathematics, including calculus, differential equations, and numerical analysis. Their study leads to deeper insights into the nature of functions and the behavior of systems. The equation `2x + 3 = 7`, mentioned in our data, is a linear example, but the principle of applying mathematical operations while maintaining balance is universal. In all these fields, the ability to solve for `x` when it's part of an `x*x*x` expression is a fundamental skill for analysis, prediction, and design.

The Role of Technology in Solving Complex Equations

While understanding the manual steps to solve equations is crucial for building foundational knowledge, modern technology offers powerful tools for tackling more complex problems, especially those where "x*x*x is equal to" a non-perfect cube or where multiple variables are involved. Equation calculators and solvers are readily available online and as software applications. These tools allow users to "enter the equation you want to solve into the editor" and "solve by best method possible." Whether you're dealing with linear, quadratic, polynomial systems of equations, or specifically cubic equations like `x*x*x = 2023`, these solvers can provide "answers, graphs, roots, and alternate forms." For instance, if you have `x*x*x = 2023`, you can input `x^3 = 2023` into a solver, and with a "click the blue arrow," it will instantly provide the numerical solution for `x`. These tools are invaluable for: * **Speed and Accuracy:** Quickly finding solutions, especially for irrational or complex roots. * **Verification:** Checking manual calculations. * **Exploration:** Graphing equations to visualize relationships and understand the behavior of functions. * **Handling Complexity:** Solving systems of equations with multiple variables or inequalities that would be cumbersome to solve by hand. The "solve for x calculator allows you to enter your problem and solve the equation to see the result," making advanced mathematical problem-solving accessible to a wider audience. This integration of technology doesn't diminish the importance of understanding the underlying math; rather, it empowers individuals to apply mathematical concepts to more intricate real-world challenges.

Beyond Real Numbers: The Intriguing World of Complex Solutions

While our focus has primarily been on finding the real-number solution for `x` in equations like `x*x*x is equal to 2`, it's important to acknowledge that cubic equations, in general, can have up to three solutions. These solutions can sometimes "blur the lines between real and imaginary numbers," as hinted in the provided data. For any cubic equation of the form `ax^3 + bx^2 + cx + d = 0`, there will always be at least one real root, but the other two roots might be complex conjugates. Complex numbers are numbers that can be expressed in the form `a + bi`, where `a` and `b` are real numbers, and `i` is the imaginary unit, defined as `√(-1)`. Consider the equation `x^3 = 1`. One obvious real solution is `x = 1`. However, there are two other complex solutions: `(-1/2) + (√3/2)i` and `(-1/2) - (√3/2)i`. While these might seem abstract, complex numbers are fundamental in fields like electrical engineering (for analyzing alternating current circuits), quantum mechanics, and signal processing. The "intriguing crossover" into imaginary numbers highlights the multifaceted nature of mathematical solutions and the richness of the number system beyond what we typically encounter in basic arithmetic. Understanding that "x*x*x is equal to" a number can sometimes lead to solutions that are not just real numbers expands our mathematical horizon and prepares us for more advanced problem-solving.

Conclusion

From the simplest algebraic expressions to the most intricate scientific models, the concept of "x*x*x is equal to" lies at the core of understanding our quantitative world. We've seen how this seemingly straightforward notation, `x^3`, represents the powerful operation of cubing, with direct links to volume and three-dimensional space. We've explored the fundamental principles of solving equations by maintaining balance and delved into specific examples like finding the cube root of 2 or 2023, revealing the presence of both rational and irrational numbers in solutions. The applications of solving equations involving `x^3` are vast and vital, impacting fields from engineering and physics to economics and chemistry. The ability to decipher these relationships allows us to design, predict, and innovate. Furthermore, we've touched upon the indispensable role of technology in solving complex equations and even glimpsed the fascinating realm where real numbers intersect with their imaginary counterparts, showcasing the depth and breadth of mathematical inquiry. Understanding "x*x*x is equal to" is more than just memorizing a formula; it's about grasping a fundamental building block of algebraic thought. It equips you with a powerful problem-solving mindset, enabling you to approach challenges systematically and uncover hidden values that drive systems and processes. Keep exploring, keep questioning, and keep solving! What other mathematical mysteries are you eager to unlock? Share your thoughts in the comments below, or explore our other articles on algebraic principles and their real-world impact.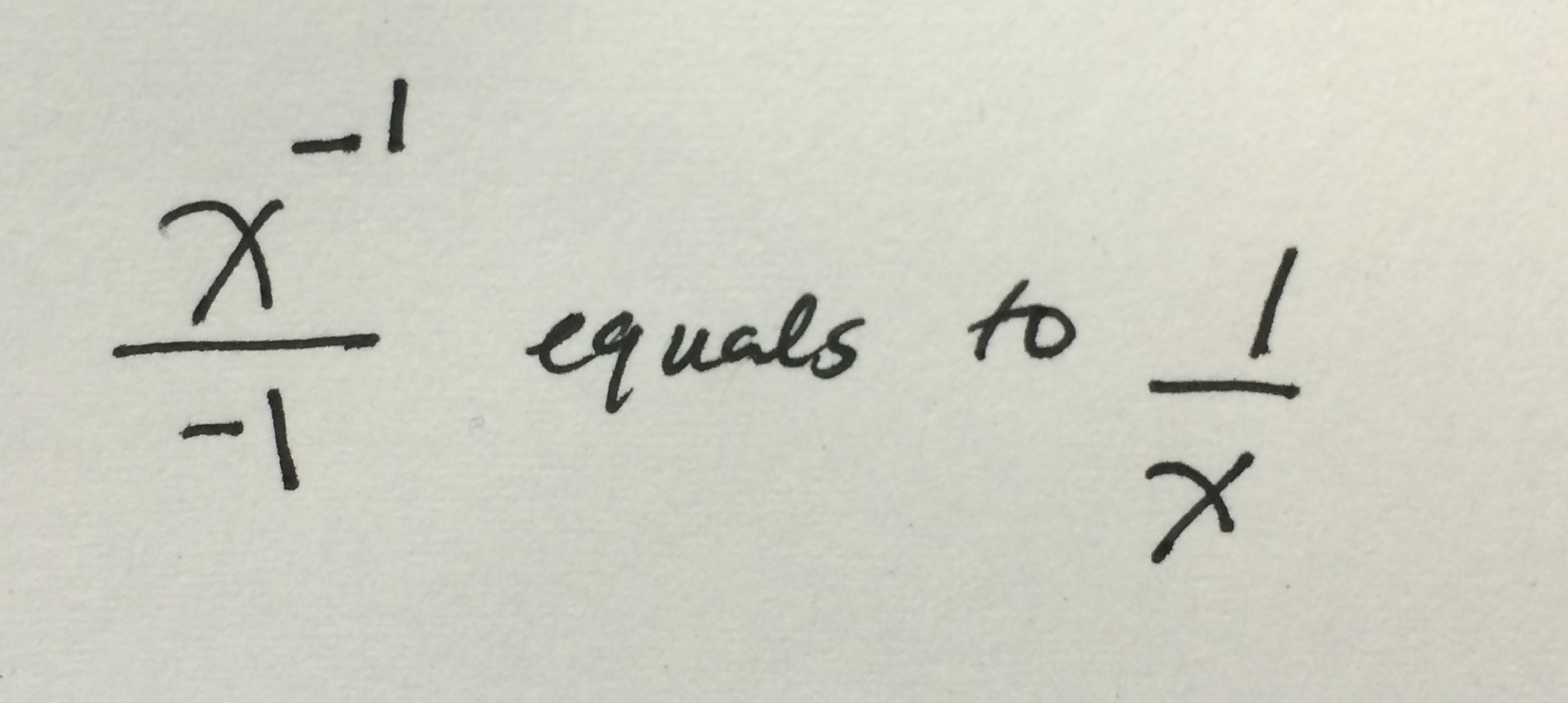

Detail Author:

• Name : Marcelle Walker
• Username : tbergstrom
• Email : ypowlowski@yahoo.com
• Birthdate : 1975-09-13
• Address : 98892 Rippin Locks Suite 224 Xavierberg, NH 43847-5557
• Phone : +1-680-504-2003
• Company : Lebsack, Kohler and Schiller
• Job : Farm and Home Management Advisor
• Bio : Occaecati aut sit velit repellendus voluptatem sed consequuntur. Ad adipisci ex aut. Id molestiae commodi ut possimus sunt.

Socials

linkedin:

• url : https://linkedin.com/in/gudrun_official
• username : gudrun_official
• bio : Natus fugit et fugit consequatur deserunt.
• followers : 6669
• following : 2219

twitter:

• url : https://twitter.com/gudrun4683
• username : gudrun4683
• bio : Molestiae sit sit aliquid voluptates dolores aut. Sit et saepe est similique reiciendis odit. Dolores fuga et et maxime nemo rem.
• followers : 443
• following : 162

instagram:

• url : https://instagram.com/gudrun_effertz
• username : gudrun_effertz
• bio : Et ut quis consequatur cumque nesciunt qui voluptatem. Tenetur mollitia quam quaerat officia.
• followers : 4716
• following : 2071